-
 牙结石怎么去除
牙结石怎么去除
其实这种物质是牙结石,它就像给牙齿和牙龈糊上了一层水泥,看似牢固,实则暗中滋生细菌,给牙齿健康埋下病根。
-
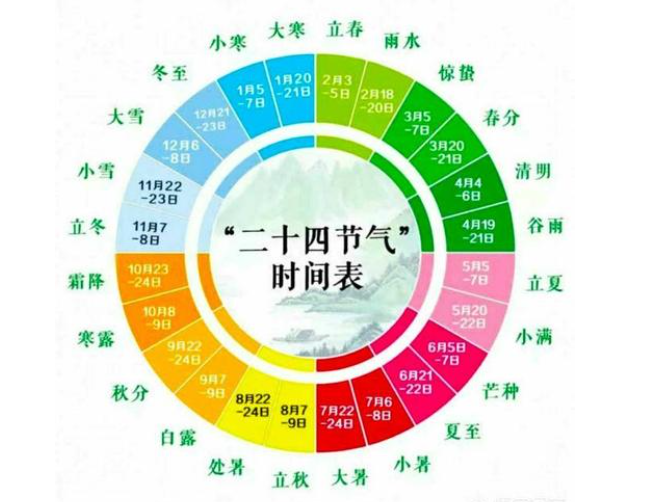 二十四节气表 24节气表图大全
二十四节气表 24节气表图大全
以前我们没有日历表来看每天时间,那是怎样确定季节的呢?那时候有二十四个节气,每6个节气是一个季节,因此大家的农事活动都是根据节气而来的。那么,二十四节气表去哪找呢?以下是万年历小编带来的24节气表图大全,一起去看看吧。
-
 泼水节是几月几号
泼水节是几月几号
泼水节是几月几号?泼水节是哪一天中国?泼水节对于我国傣族人民来说是新年的存在,因此节日很是隆重,每年都要安排假期来举办和参与活动,当然这只是部分公民享有,但是节日氛围吸引了海内外所有人来参与,可见其活动的盛大,接下来和万年历小编一起去看看吧。
-
 适合长期不换的网名
适合长期不换的网名
我们其实都不是薄情寡义的人,只是专一了一段时间而已,但是不能说没有长情的人,终身挚爱一人,一生只用一个网名的人大有存在,只不过我们身边少见而已。
-
 谷雨的诗句鉴赏 谷雨的著名诗句
谷雨的诗句鉴赏 谷雨的著名诗句
导语:谷雨节气是二十四节气中的第六个节气,也是春季最后的一个节气。谷雨节气的来临意味着暮春时节,雨水也渐渐增多了,有了春雨的滋润万物清新,是个适合作诗的好时节。因此有很多谷雨的著名诗句流传,下面就让我们一起来看看谷雨最有名的诗鉴赏。
-
 射手座男生性格特点
射手座男生性格特点
射手座男生的性格特征:1、情似火,重情仗义:热情,乐观,总是给人一种错觉,好像认识很久的朋友似的,即使可能连对方名字都叫不上来,他都能非常热情健谈的和对方展开一系列的交谈。2、性格外向直爽,无论在任何场合,幽默直爽的射手男都能创造一个轻松、欢笑的氛围。3、讨厌被束缚,自我:对于喜欢的人,无论有多少好感,只要是对方要求他要求的太多了,控制欲太强了,希望和他一天到晚腻在一起,射手男一定会挥剑斩情丝。
-
 白羊座男生性格特点
白羊座男生性格特点
说起白羊座男人的性格标签,我们首先会想到的就是直来直去,爱憎分明,甚至风风火火的白羊座男人,因为凡事都喜欢追求所谓的速度,很多时候并不会在乎其过程是否完美,但白羊座男人还有哪些典型的性格特点呢,下面我们就来分析下白羊座男人性格特征。
-
 双子座男生性格
双子座男生性格
在双子男典型性格特点中,比较广为人知的就是双子座随机应变的能力,当然这也跟双子座的守护星水星有着分不开的关系,只是需要说明的是,因男生和女生在性格上有着很大的不同,那么,双子座男人性格特征又有哪些不同呢?下面我们就来详细解析下双子座男生的性格。
-
 京地铁运营时间 北京地铁运营几点到几点
京地铁运营时间 北京地铁运营几点到几点
北京的地铁为北京通行带来了好的方式,虽然北京地铁人特别多,但是大家也因为地铁去哪都方便起来,不过北京地铁线路颇多,路线复杂,运营时间也不一样,那么北京地铁运营时间是怎么样的呢?想知道北京地铁运营几点到几点,就来看看万年历小编的介绍吧。
-
 申时是几点到几点
申时是几点到几点
在我们的生活中,全国都是统一使用北京标准时间,然而在古代我们用时辰来计算时间,远没有现在钟表方便。现在的年轻多数都不懂用时辰来计时,例如十二时辰中的申时,你知道申时是什么